15 aug. 2023
4 minuten
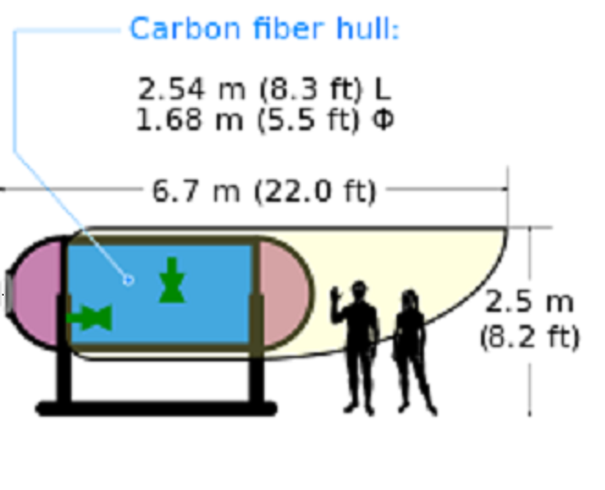
Het is alweer twee maanden geleden dat de Titan submersible van de radar verdween. Intussen weten we dat de gelamineerde koolstofromp is bezweken onder de druk van het water. Gepensioneerd Ir Werktuigbouwkunde Freek Hooning maakte een analyse van het ontwerp, grotendeels bestaande uit een sterkteberekening. Wat zijn volgens hem de oorzaken van het ongeval?
Door: Freek Hooning
Verscheidene mogelijke oorzaken van deze ramp zijn door diverse experts al onder de aandacht gebracht, zoals het minder geslaagde ontwerp van de CFRP romp, dat eventueel tot een implosie van het centrale deel van de romp zou kunnen leiden of de opvallend lage sterkte van de patrijspoort. Uit de reddings- en tevens bergingsoperatie, die werd uitgevoerd nadat het ongeluk had plaatsgevonden, is gebleken dat beide gebeurtenissen zich hadden voltrokken: de romp was geїmplodeerd en de patrijspoort was compleet verdwenen uit de halve titanium bol aan de voorzijde van de duikboot. De belangrijkste vraag is nu:
Wat gebeurde er eerst en is er een verband tussen beide gebeurtenissen?
Onderzoek, deel 1
Eerst is de betrouwbaarheid van de CFRP romp onderzocht. Voor een cilinder zijn de hoofdspanningen (zie [ref. 1]) de hoepelspanning (σ1) en de axiale spanning (σ2) met σ1 = pr/t en σ2 = pr/2t.
En zodoende: σ1 = 40 * 1.550 / 127 = 490 MPa en σ2 = 245 MPa. Vanzelfsprekend zijn beide spanningen drukspanningen. Uit de ‘eenvoudige laminaat theorie’ [ref. 5] kunnen gemiddelde toelaatbare drukspanningen worden afgeleid: σ1 = 825 MPa en σ2 =800 MPa
In eerste instantie is er dus nog geen enkele reden om zich zorgen te maken over de veiligheid van dit ontwerp.
Onderzoek, deel 2
Vervolgens is de betrouwbaarheid van de uit PMMA vervaardigde patrijspoort onderzocht. Uit een uiterst informatief You Tube filmpje van CBS News kan worden opgemaakt dat de patrijspoort bolvormig is geconstrueerd:
Daarom is eerst bepaald of een acrylaat bol met een wanddikte van 7 inch überhaupt in staat is een druk van 400 bar te weerstaan. Uitgaande van een maximaal toelaatbare drukspanning van 120 MPa [ref. 3] en gebruik makend van de formule pr = σt / 2 (zie weer [ref. 1]) werd een waarde van r = σt / 2p = 120*178 / 80 = 267 mm voor de maximaal toelaatbare straal verkregen. Dit impliceert een maximale diameter voor de patrijspoort van 2*267 mm = 53,4 cm, terwijl de werkelijke diameter ca. 53 cm bedraagt. Het lijkt er dus op dat de patrijspoort een druk van 400 bar kan weerstaan, maar dan wel zonder enige reserve, terwijl het in een dergelijke kritieke situatie natuurlijk dringend gewenst is dat er een veiligheidsfactor (van bijvoorbeeld 3) in de berekening wordt meegenomen.
Hierna zijn de maximale schuifspanning (die optreedt bij de ondersteunde buitenrand van de patrijspoort) en de maximale binnenwaartse verplaatsing van het middelpunt van de patrijspoort onderzocht. Tot nu toe is er steeds vanuit gegaan dat de patrijspoort een convexe (bolle) vorm heeft, hetgeen gunstig is omdat de druksterkte van PMMA ongeveer 70 % hoger is dan de treksterkte. Het is derhalve van groot belang dat de patrijspoort onder de immense druk van 400 bar zijn convexe vorm behoudt en niet omslaat naar een concave (holle) vorm.
Teneinde deze berekeningen op een niet al te ingewikkelde manier te kunnen uitvoeren is gebruik gemaakt van majorering, waarbij de patrijspoort modelmatig wordt voorgesteld als een 20 mm brede balk met een doorbuiging van 0 graden in het midden. Het voordeel van een dergelijke aanpak is dat een aantal indicatieve resultaten (die een bovengrens stellen aan de berekende waarden) kunnen worden verkregen, hetgeen deze analyse vergemakkelijkt. Gebruikmakend van de bekende formule uit de balkentheorie: Δy = ql4/8 EI en uitgaande van:
- q = 800 N / mm
- l = 265 mm
- E = 2,9 GPa
- I = (1 / 12) bh3 = 9.400.000 mm4
werd voor de binnenwaartse verplaatsing een waarde gevonden van ongeveer 18 mm. Een relatief eenvoudige goniometrische berekening laat zien dat de convexe vorm van de patrijspoort omslaat in een concave vorm, zodra de binnenwaartse verplaatsing van het middelpunt een waarde van ongeveer 25 mm overschrijdt. Omdat de berekende waarde van 18 mm een bovengrens stelt, is het duidelijk dat zelfs onder een druk van 400 bar de convexe vorm niet in gevaar komt.
D.m.v. de formule: V(x) = 212.000 – 800 x
Kan de maximale schuifspanning worden berekend:
τmax = 212.000 / 20*178 = 60 MPa
Het is zeer wel denkbaar dat de patrijspoort een dergelijke schuifspanning (althans voor korte tijd) kan weerstaan, maar ook hier is er geen enkele ruimte voor een veiligheidsfactor, hetgeen onder dergelijke kritieke omstandigheden toch ten zeerste moet worden aanbevolen.
Conclusies
- Het lijdt geen twijfel dat de patrijspoort het zwakke punt is van dit ontwerp en er kan ook nauwelijks twijfel over bestaan dat de patrijspoort zal bezwijken nog voordat een eventuele implosie van de CFRP romp zal plaatsvinden. Echter, een CFRP laminaat is uitermate kwetsbaar voor blootstelling aan een hoogenergetische impact-belasting (stootbelasting), die zeker zal volgen zodra de patrijspoort is bezweken.
- De slotconclusie luidt dan ook dat na enige tijd (niet noodzakelijkerwijs al bij de eerste duikvaart) de teloorgang van zowel de patrijspoort als de CFRP romp onontkoombaar is, waarbij het bezwijken van de patrijspoort onmiddellijk ook de implosie van de romp teweeg zal brengen.
Referenties
- S. Timoshenko, Theory of Plates and Shells, Mc Graw-Hill Book Company, Inc., New York and London, 1940.
- https://en.wikipedia.org/wiki/Titan_submersible_implosion, achtergrondinformatie, met name over de mogelijke implosie.
- https://en.wikipedia.org/wiki/Poly(methyl_methacrylate), bevat informatie over de thermoplastische kunststof PMMA.
- https://docplayer.nl/4164107-Vuistregels-ontwerpen-met-composieten, waarin o.a. de eenvoudige laminaat theorie wordt behandeld.
- Schematische tekening van de Titan, zoals in de afbeelding is weergegeven.
Het laatste nieuws
Geef een reactie
Reacties (8)
Anderen lazen ook
in het artikel staat dat het ontwerp de druk kan weerstaan en ook een optredende schuifspanning. Ik snap (als geïnteresseerde leek) niet dat dan toch de conclusie is dat na enige tijd de teloorgang van zowel de patrijspoort als de CFRP romp onontkoombaar is.
Kennelijk is er meer dat een rol speelt, wat dat is zou ik graag willen weten.
Beste Jabik,
Bij een herhaalde belasting treedt vermoeiing op, waardoor de toelaatbare spanningen afnemen en de constructie al eerder bezwijkt. Het gevolg is dus dat de constructie niet meteen bij de eerste de beste duik bezwijkt, maar pas bij een van de latere duikvaarten.
Met vriendelijke groet,
Freek Hooning
Is het mogelijk om prototype vaartuigen onbemand met camera’s en sensoren waarmee de data in een soort black box zoals in vliegtuigen gebruikelijk is worden weg geschreven. Deze onderzeeër een duik op een locatie laten maken die dieper is dan het ontwerp voor bedoeld is. Wanneer deze implodeert dat deze black box die zich b.v. aan de buitenzijde bevind dan loskomt en naar de oppervlakte kan opstijgen met een baken zodat deze gegevens geanalyseerd kunnen worden. Men weet dan tevens dat de veiligheid marges voldoende of onvoldoende zijn. Graag reactie op dit idee of dit al gebeurd of mogelijk is.
Beste Wim,
Wat jij voorstelt is zeker een interessant idee en het lijkt mij ook prima uitvoerbaar, maar het is mij niet bekend of dit al geprobeerd is.
Met vriendelijke groet,
Freek Hooning
Hmmmmm, mmmja. Dat is de theoretische benadering die bij de bouw ook wel gebruikt is. Geen nieuws. Deze benadering vergeet minstens drie feiten
1. Bij de de verlijming van de CF romp aan de titaniumring is de ring niet voldoende ontvet en de lijm niet in vacuüm ontlucht. Dit blijkt duidelijk uit de filmpjes van de bouw van Titan. De lijmverbinding was dus onvoldoende sterk en zonder de ring is de sterkte van de CRFP-romp betekenisloos.
2. Het CRFP-laminaat was niet kruislings verlijmd en dat betekent dat alle vezels maar in één richting liepen. Daardoor kon eventuele schade zich makkelijk voortplanten langs de vezels.
3. Het CRPFP-laminaat herstelt niet zoals metaal herstelt na belasting. Eenmaal gebroken vezels zijn verloren voor de sterkte. Bemanningen klaagden bij eerder duiken over het voortdurende gekraak van de romp. Natuurlijk was dat het gevolg van compressie en decompressie, maar daarbij werden vezels beschadigd en liep de sterkte terug. Omdat daarmee de overgebleven vezels steeds zwaarder belast werden, was het verlies aan sterkte exponentieel progressief.
Beste Rene,
Hartelijk dank voor je aanvullende opmerkingen, die ik zeker ter harte zal nemen!
Met vriendelijke groet,
Freek Hooning
Beste heer Honing,
Ik stuitte bij toeval op uw artikel. Het ongeluk met de Titan en de vraag naar de oorzaak heeft eveneens mijn interesse als ingenieur gewekt.
Als we aannemen dat dergelijke zaken niet door leken worden ontworpen en gebouwd, dan is misschien wel juist de onbegrepen complexiteit van het faalmechanisme van dergelijke constructies de oorzaak ervan.
Eerlijk gezegd mis ik dit aspect in uw analyse, maar wat veel erger is, ook uw (te) eenvoudige analyse lijkt ernstige rekenfouten te bevatten. Daarom – in het belang van ons vakgebied – hieronder mijn kanttekeningen en overwegingen:
– Voor de cilindrische romp gebruikt u de zogenaamde ketelformule buiten haar geldigheidsdomein (R>20t). De wanddikte bedraagt 5” (127 mm) bij een binnendiameter van 1420 mm. Daarmee komt de gemiddelde diameter op 1420+127=1547 mm.. door u afgerond op 1550 mm. R/t is daarmee 1547/2/127 = 6.1!
Voor dergelijk vaten dienen de formules voor dikwandige vaten gebruikt te worden waarin de gradiënt van de spanning over de wanddikte is verdisconteerd.
– Afgezien van het feit dat uw formule niet correct is, is ze wel een benadering voor de gemiddelde spanning. De (benaderde) gemiddelde hoepelspanning bedraagt dus σ1= p·r/t = 40*1550/2/127 = 244 MPa terwijl de axiaalspanning σ2=p·r/2t= 122 MPa bedraagt.. Ik vrees dat u er een factor 2 naast zit, aangezien diameter voor straal is ingevuld.
– De radiale belasting σ3 is bij een druk van 400 bar geen verwaarloosbare parameter. Deze bedraagt aan het buitenoppervlak 40 MPa.
– Het kritieke punt in dergelijke onder externe druk staande cilinders is meestal niet de sterkte, maar knikstabiliteit. Een belangrijke parameter daarin is de elasticiteitsmodulus van het materiaal. Dit is vrijwel zeker het bezwijkmechanisme van de Titan geweest. Knik is een instabiliteits-verschijnsel en het effect is een implosie.
– De Titan was geconstrueerd uit verschillende materialen. (PMMA, CFRP, Titanium)
o Deze materialen hebben verschillen in thermische uitzetting. Dit veroorzaakt thermische spanningen als de constructie bij een andere temperatuur wordt ingezet (het is ongeveer 2° vanaf 1000 meter diepte) als waaronder deze is geassembleerd (waarschijnlijk kamertemperatuur).
o De materialen hebben verschillen in Elasticiteitsmodulus en zullen ten gevolge van dezelfde belasting verschillend willen vervormen. Dit wordt vooral zichtbaar in de zones waar de materialen met elkaar verbonden zijn.
– Tot slot iets over het Composiet. Als (interne) delaminatie is opgetreden dan zal dit met name de stabiliteit van de wand sterk beïnvloeden en daarmee de knikstabiliteit van de cilinder.
Het feit dat de Titan zijn Waterloo heeft gevonden na meerdere duiken te hebben gemaakt, maakt dit een plausibel scenario. Dergelijk delaminatie kan talloze oorzaken hebben, waaronder uiteraard (hier vooral hydraulische) mechanische belasting, materiaalveroudering, maar ook snelle decompressie waarbij gassen die in de matrix zijn doorgedrongen onder druk gaan expanderen bij decompressie en interlaminaire spanningen veroorzaken die hoger zijn dan de bindingssterkte.
– Voor de bolvormige patrijspoort gebruikt u eveneens een formule die alleen geldig is voor dunwandige constructies, maar afgezien daarvan lijkt daar ook een vervelende fout in te zijn geslopen: σ1= σ2 = pr/2t.–> Rmax = σtoelaatbaar·2·t/p. Gebruikmakend van uw σtoelaatbaar = 120 MPa zou dit een Rmax opleveren van 1067mm oftewel 4x hoger dan de door u berekende 267 mm..
Kortom: Uw conclusie lijkt gebaseerd op verkeerde berekeningen en de hele zaak lijkt me veel ingewikkelder dan uw artikel suggereert.
Mocht mijn analyse de proef doorstaan, dan is het wellicht raadzaam dit artikel offline te halen. Het is wat kort door de bocht, maar dergelijke ‘onwetenschappelijke acrobatiek’ is ook een van de oorzaken van technische ongelukken.
Ik ga morgen (di 29.05.2025) in ieder geval de documentaire op BBC2 zeker kijken!
m.vr.gr. Gesinus Mateman
Oprechte vraag: ik ben electronicus, dus niet ingevoerd in deze materie. Voor zover mijn kennis strekt, zijn vezels in een cylinder- of vatvorm uitstekend bestand tegen druk van binnen naar buiten. Bij LPG tanks en ook waterstof tanks (zeer hoge druk) wordt dan ook deze vezel/composiet constructie toegepast. Bij deze sub was de druk van buiten naar binnen en dan is het opeens een boogcontructie. Mijn gevoel (nogmaals, geen deskundige op dit gebied) zegt dat 400 bar IN de cylinder prima zou werken, maar 400 bar OP de cylinder was een ‘accindent waiting to happen’. Wellicht kan iemand mij aangeven of dit meegespeeld heeft?