Megaohmmeters op batterijen. Het aanbod werkplaatsuitrusting van TME omvat onder meer professionele apparaten van Fluke. Onlangs is dit assortiment uitgebreid met nieuwe draagbare isolatieweerstandste[…]
Meer…De HCX oliepeilglazen van Elesa+Ganter bieden een geavanceerde oplossing voor industrieel onderhoud en productie. Deze serie is essentieel voor precieze metingen en de betrouwbaarheid van apparatuur. […]
Meer…Een kleinschalig en compact apparaat, Fuze, gebouwd door de Amerikaanse startup Zap Energy heeft plasma elektron temperaturen bereikt van 1-3 keV (zo’n 11 tot 37 miljoen graden Celsius). In de b[…]
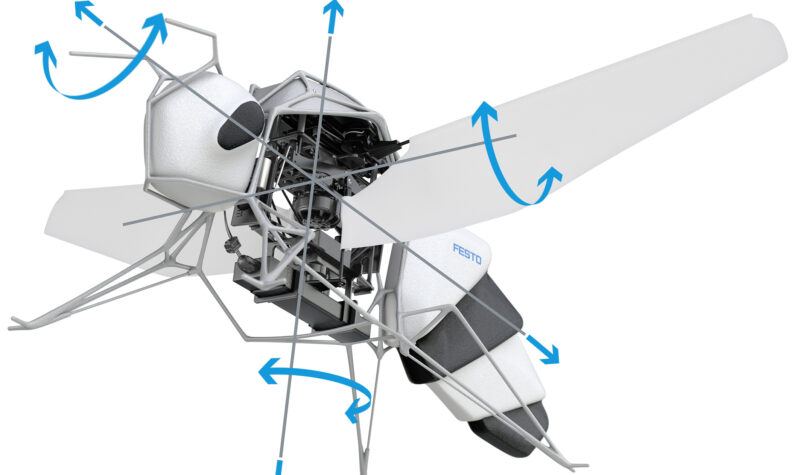
Meer…Al 15 jaar is het Festo Bionic Learning Network gefascineerd door vliegen. Het team heeft talrijke vliegende objecten en hun natuurlijke principes onderzocht en technologisch geïmplementeerd. Met de […]
Meer…Kwantummechanische verschijnselen zoals radioactief verval, of algemener: ‘tunnelen’, vertonen intrigerende wiskundige patronen. Twee onderzoekers aan de Universiteit van Amsterdam hebben laten zi[…]
Meer…Een nieuwe ultragevoelige glasvezelsensor kan deeltjes met een diameter tot 50 nanometer detecteren. In de toekomst zal deze sensor worden ingezet voor een betere luchtkwaliteit in scholen. Een klasse[…]
Meer…Siemens Nederland en VDL Automated Vehicles lanceren dit najaar de tweede generatie van hun geautomatiseerd logistiek platform op basis van Automated Guided Vehicles (AGV’s) voor industriële bedrij[…]
Meer…Voor de productie van waterstof zijn elektrolysers nodig, maar de integratie van deze installaties in een toch al overbelast elektriciteitsnetwerk is niet eenvoudig. Bart de Vries, Business Developer […]
Meer…In 2023 kreeg bijna driekwart van de Nederlandse bedrijven te maken met een cyberaanval. Dat stelt ABN Amro na onderzoek onder 895 organisaties. ‘Ondanks het hoge dreigingsniveau blijft de risic[…]
Meer…Om het concurrentievermogen van Europese ruimtetransportsystemen te vergroten, ontwikkelen onderzoekers van het Fraunhofer Instituut voor Lasertechnologie (ILT) innovatieve productietechnologieën voo[…]
Meer…