
Een uraniumkristal geeft al 35 jaar zijn geheim niet prijs. Wat veroorzaakt de dramatische fase-overgang bij 17,5 Kelvin? Dankzij gebruik van AI valt nu de helft van de mogelijke verklaringen af, maar de definitieve oplossing lijkt nog altijd ver weg. “Het is echt heel frustrerend”, zegt 82 jarige natuurkundige John Mydosh.
Het begon zo veelbelovend: In de jaren tachtig krijgen vastestof-fysicus John Mydosh en zijn Leidse collega’s beschikking over een reeks uranium-houdende kristallen. Uranium is niet alleen van belang voor kernfysica, maar is ook een reuzenatoom met een elektronenschil van 235 elektronen, wat wel eens tot exotische verschijnselen kan leiden in uraniumkristallen.
En inderdaad, bij het kristal uraniumrutheniumsilicium (URu2Si2) was het raak. "Als je het afkoelt tot 17,5 Kelvin zie je duidelijk een fase-overgang’" zegt Mydosh, een van oorsprong Amerikaanse natuurkundige die is verbonden aan de universiteit Leiden. "Maar wat is de oorzaak?" Mydosh en collega’s publiceren in 1985 een veelgeciteerd artikel in Physical Review Letters, waarin de fase-overgang in het uraniumkristal wordt verklaard als antiferromagnetisme, ofwel een variant op magnetisme. Case closed. "Alleen: er klopt helemaal niets van."
De theorie van fase-overgangen schrijft voor dat er altijd een orde-parameter is onder de overgangstemperatuur. Bij het bevriezen van water is dat bijvoorbeeld de mate van geordendheid van de moleculen. Mydosh: "Maar wat is hier de orde-parameter? Het is geen magnetisme, geen verandering in het kristal, geen supergeleiding. We weten het niet, daarom noemen we het dus een ‘Verborgen Orde’."
Extra intrigerend is dat URu2Si2 bij 1,5 Kelvin een nieuwe fase-overgang laat zien, deze keer naar een supergeleidende toestand. De twee fase-overgangen lijken bovendien met elkaar te maken hebben. "Als je de verborgen orde-overgang uitschakelt, bijvoorbeeld onder hoge druk, verdwijnt de supergeleidende overgang ook", zegt Mydosh.
Frustratie
Inmiddels zijn er meer dan duizend publicaties over het probleem verschenen, waarin tientallen theorieën gelanceerd worden. Maar geen daarvan is breed geaccepteerd. "Twee jaar geleden, toen ik nog jong was, zijn we een hele week naar het synchrotron in Hamburg geweest om te meten met een hypothese. Dat is slopend hoor, dag en nacht ben je bezig. Maar goed, we hebben het niet kunnen publiceren, en we hebben ons negatieve resultaat nooit gepubliceerd. Een enorme frustratie."
AI
En nu is er een artikel in Science Advances , waarbij een neuraal netwerk wordt ingezet. "AI is in de mode, dat is hip hop", zegt Mydosh. "Zelf snap ik daar niet veel van". Maar co-auteur Eun-Ah Kim van Cornell University in New York is een expert. De onderzoekers gebruiken Resonant Ultrasound Spectroscopy (RUS), een techniek waarbij het uraniumkristal in een holte vastgeklemd wordt tussen twee ultrageluid-elementen. Het ene element stuurt ultrageluidstrillingen met frequenties van honderdduizenden trillingen per seconde het kristal in. Het andere element detecteert de sterkte van de trillingen die door het kristal heenkomen.
Het proces is te vergelijken met het bekloppen en beluisteren van een materiaal. Metaal geeft een heldere ‘ting’, hout is meer ‘pok’, en glas klinkt toch ook weer net iets anders. Ieder kristal heeft een aantal resonantiefrequenties, die bepaald worden door de elastische constanten, de manier waarop de atomen trillen door de krachten tussen die atomen. Door de resonanties te volgen terwijl de temperatuur varieert, is de fase-overgang ook te zien is. Sommige resonanties laten een u-vormige knik zien, andere een s-vormig kuiltje in hun frequentiecurve.
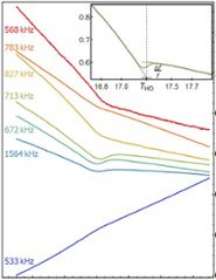 Grafiek van de resonanties die afhankelijk zijn van de temperatuur. De groene en blauwe curves laten een s-bocht zien, de andere een u-bocht
Grafiek van de resonanties die afhankelijk zijn van de temperatuur. De groene en blauwe curves laten een s-bocht zien, de andere een u-bocht
U- en S-bochten
Aan de hand van die knikken en kuilen is weer iets te zeggen over de geheimzinnige fase-overgang. De theorieën daarvoor zijn in te delen in twee hoofdtypen: theorieën waarbij de verborgen ordeparameter een enkel getal is, en theorieën waarbij de ordeparameter twee componenten heeft. Bij die laatste klasse zouden meer curven kuiltjes moeten hebben dan bij de één-component-theorieën.
Een praktisch probleem is daarbij wel dat de grootste kristallen, met het duidelijkste signaal en een mooie, eenduidige vorm, niet zo’n goede kristalstructuur hebben, wat het spectrum kan vertroebelen. Kleinere kristallen hebben wel een mooie, enkelvoudige kristalstructuur, maar geven minder signaal, en het is lastiger om in ze de juiste vorm te polijsten voor een goede RUS-analyse.
Dit betekent dat het resonantiespectrum in beide gevallen niet zo gemakkelijk te interpreteren is: het ontbreken of onduidelijk zijn van slechts één resonantiefrequentie kan de hele analyse in de war gooien. De vertaling van kuiltjes en knikjes naar een ordeparameter is daardoor erg ondoorzichtig. Hier kan kunstmatige intelligentie uitkomst bieden.
Kunstmatig Neuraal Netwerk
Daar staat tegenover dat vertaling in de andere richting goed te doen is. Een computer kan gemakkelijk een kristal simuleren, inclusief vorm, temperatuur en een fase-overgang met een één- of tweecomponenten- ordeparameter. Terwijl de temperatuur varieert, berekent het model het verloop van de resonantiefrequenties.
Om die route om te keren, gebruikten de onderzoekers een kunstmatig neuraal netwerk, een vorm van Kunstmatige Intelligentie losjes gebaseerd op de werking van hersencellen. Om patronen te erkennen moeten neurale netwerken, net als sporters of huisdieren, getraind worden.
Aan de ene kant gaat een gesimuleerd spectrum het neurale netwerk in, aan de andere kant rolt er een antwoord uit: één of twee componenten. Als dat antwoordt klopt, worden de verbindingen tussen de hersencellen versterkt, als het niet klopt, worden ze aangepast. Door dit duizenden malen te herhalen leert het netwerk het patroon te herkennen dat bij een één- of een tweecomponenten parameter hoort. De onderzoekers voerden de robuustheid van die patroonherkenning nog eens op door willekeurig frequenties uit het spectrum weg te knippen, zodat het ook voorbereid zou zijn op niet-perfecte metingen, waarin resonantiefrequenties zijn weggevallen.
Kandidaat-theorieën
Toen het netwerk na duizenden oefenrondes het determineren van gesimuleerde kristallen een keer onder de knie had, voerden de onderzoekers het met echte meetgegevens. Daar wist het wel raad mee: dat waren duidelijk spectra van faseovergangen met een ordeparameter van één component.
"Het blijkt dat de patronen heel duidelijk van elkaar te onderscheiden zijn", zegt Mydosh. "Van de twintig kandidaat-theorieën valt daarmee de helft af, dus er blijven er zo’n tien over om verder te testen."
Dat is mooi, al is het mysterie daarmee bepaald nog niet opgelost. Maar, schrijven de auteurs, de aanpak kan veel breder gebruikt worden. "Ieder probleem waarbij de simulatie van een dataset gemakkelijk is, maar het fitten lastig, zou vatbaar moeten zijn voor deze aanpak."
En John Mydosh, die speurt intussen verder.
Bron: Universiteit Leiden




