Stevigheid, is dat een materiaaleigenschap?

Door Erik Tempelman, oprichter/eigenaar van eriktempelman.com, universitair hoofddocent, TU Delft, Industrieel Ontwerpen

Het bijvoeglijk naamwoord ‘stevig’ gebruiken we doorgaans in de betekenis van ‘nogal groot’. Denk maar aan zinsneden als ‘een stevige maaltijd’ of ‘een stevige ruzie’. Het woord beduidt ook robuustheid en betrouwbaarheid: een stevige constructie zal niet snel falen, zelfs niet bij gebruik buiten de specificaties. U staat ook liever op een stevige keukentrap dan op eentje die slap of wankel aanvoelt. Constructeurs spreken, evenals hun klanten, verder vaak van ‘een stevig materiaal’. Echter, bij de materiaalkundige gaan dan de alarmbellen rinkelen. In tegenstelling tot stijfheid en sterkte is stevigheid namelijk geen formele materiaaleigenschap.

Kerftaaiheid

Gelukkig gaan er dieper in de materiaalkunde enkele begrippen verborgen die de informele betekenis goed afdekken. Om daar te komen, lichten we eerst het begrip kerftaaiheid toe. De kerftaaiheid (Engels: fracture toughness ) is een maat voor de maximale spanning σ_c die een materiaal kan weerstaan in aanwezigheid van een kleine, scherpe kerf, zonder dat het materiaal bros faalt. Bros beduidt dan falen zonder merkbare plastische deformatie – het omgekeerde van taai, en vandaar de naam.

Kerftaaiheid wordt doorgaans aangeduid met het symbool K_Ic . De K verraadt de verwantschap met spanningsconcentratiefactoren, waarbij we deze letter ook tegenkomen; de I duidt op de richting van de spanning¹ en de c staat voor critical. Hoe groter de kerf, hoe lager de spanning, zo blijkt uit tests. Er bestaat bovendien een specifieke relatie tussen beide variabelen, waardoor de kerftaaiheid van een materiaal onafhankelijk van de proefstukgrootte kan worden bepaald. De vorm van de kerf is ook nog licht van invloed, maar ook daar is systematisch voor te corrigeren. Dit samen maakt dat we hier met een echte materiaaleigenschap te maken hebben, onafhankelijk van grootte of vorm van het proefstuk in kwestie. In formule hebben we:

K_Ic = Y·σ_c·√(π·a)

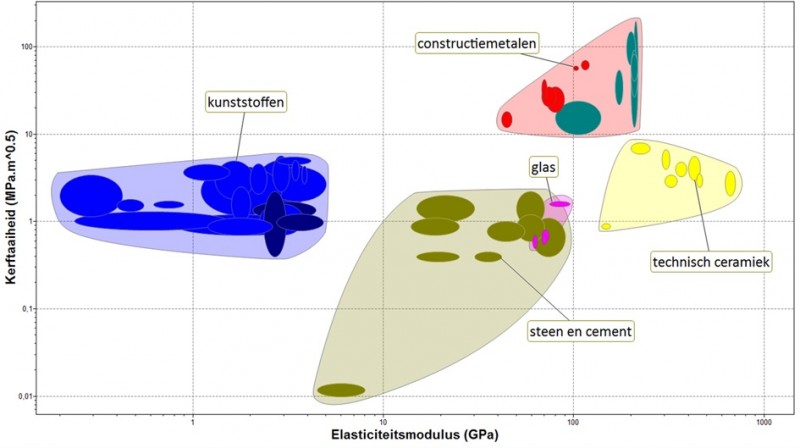
Hierin is Y een vormfactor, doorgaans min of meer gelijk aan 1, σ_c de faalspanning en a de lengte van de kerf. Dimensieanalyse leert ons dat kerftaaiheid de ogenschijnlijk eigenaardige eenheid heeft van MPa·√m. Afbeelding 1 laat het typische bereik zien van deze grootheid per materiaalgroep, met de elasticiteitsmodulus als referentie. Merk op hoe groot het totale bereik voor beide grootheden is: liefst vier decaden!

‘Buigen voor het barst’

Kerfjes, hoe klein ook, zijn in de constructiepraktijk nooit uit te sluiten: wat dat aangaat zijn ze vergelijkbaar met spanningsconcentraties. Wanneer ze niet in de constructie zelf voorkomen, dan zitten ze – enkele ordes van grootte kleiner – wel in het materiaal, bijvoorbeeld als krimpscheuren in gietwerk². Waar het in de praktijk om gaat is of de brosse faalspanning σ_c hoger is dan de vloeigrens van het materiaal: dan zal het materiaal namelijk ‘buigen voor het barst’. Het omgekeerde is uiteraard onwenselijk, want in dat geval wordt niet alleen de vloeigrens (lang) niet gehaald, maar is de faalvorm ook gevaarlijker: bros in plaats van taai.

De formule leert ons dat, bij een kerflengte a = 1 mm, σ_c ≈ 18·K_Ic ; is a = 10 mm, dan geldt σ_c ≈ 6·K_Ic. Samen met afbeelding 1 verklaart dit waarom veel kunststoffen, ondanks hun lage kerftaaiheid, vaak toch taai breken: hun vloeigrens is namelijk maar zo’n 20-50 MPa. En, het verklaart waarom kerftaaiheid binnen de traditionele werktuigbouwkunde relatief onbekend is. Constructiestaal is met een K_Ic ≥ 50 MPa·√m namelijk dermate kerftaai dat zelfs bij diepe kerven de σ_c nog boven de vloeigrens ligt, en dus niet maatgevend is voor het faalgedrag³.

Vloeigrens of kerftaaiheid?

Om te zien of de vloeigrens dan wel de kerftaaiheid maatgevend is, kunnen we in de genoemde formule de vloeigrens σ_yield substitueren voor de kritieke spanning σ_c . Met Y = 1 krijgen we dan a_c = K_Ic²/(σ_yield²·π). De resulterende grootheid a_c is de scheurlengte waarbij we van het taaie faalregime naar het brosse faalregime gaan. Voor standaard ‘staal 52′ constructiestaal geldt dat a_c ≈ 9 mm en daarmee is het materiaal beslist goed bestand tegen brosse breuk.

Het dient nog gezegd dat de kerf klein moet zijn ten opzichte van de constructie teneinde de effectief werkzame doorsnede niet merkbaar te verminderen: voor bijvoorbeeld een kerf van zo’n 10 mm in een 30-mm dikke constructie is dit natuurlijk niet het geval. Kerfjes kunnen overigens ook bewust worden aangebracht om, dankzij een lage kerftaaiheid, een (zeer) lage faalspanning te creëren, en wel op een specifieke plaats. Stratenmakers tikken zo menig baksteen in tweeën, en plastic zakjes voor ketchup, shampoo en aanverwante goederen worden makkelijker te openen.

Via energieopname…

Een stevig materiaal, zo kunnen we afleiden uit het alledaagse gebruik van de term, is allereerst een materiaal dat ‘tegen een stootje kan’. Materiaalkundig gezien betekent dit een materiaal dat, per eenheid volume, relatief veel energie kan opnemen voordat het bezwijkt. Voor taaie materialen kunnen we deze energieopname W afleiden uit de trekproef: de gezochte grootheid is namelijk het oppervlak onder de trekkromme. Moet deze opname reversibel zijn, dan moeten we ons beperken tot het elastische regime. De Wet van Hooke voorspelt hiervoor dat het oppervlak onder de trekkromme dan maximaal gelijk is aan W_el = ½·σ_yield²/E . Hierin is σ_yield opnieuw de vloeigrens van het materiaal en is E de elasticiteitsmodulus. Bij irreversibele opname komt ook het plastische regime in beeld: in eerste benadering is dit W_pl = ½·(σ_yield + σ_ultimate)·ε_max . In deze uitdrukking is σ_yield nogmaals de vloeigrens, σ_ultimate de treksterkte en ε_max de breukrek van het materiaal. De eenheden zijn in beide regimes gelijk aan N/m², oftewel arbeid (N·m) per eenheid volume (1/m³). Zeker bij metalen geldt overigens dat W_pl >> W_el .

…naar toughness

Een stevig materiaal verdraagt een stootje niet eenmalig, maar herhaaldelijk, en dat maakt dat alleen elastische vervormingen toegestaan zijn. Aanwezigheid van kleine beschadigingen, zoals kerfjes, mag verder geen probleem vormen. We kunnen dan nog steeds naar de specifieke energieopname kijken, maar nu, simpel gezegd⁴, met de kerftaaiheid als vervanger voor de vloeigrens. De resulterende grootheid is de toughness , doorgaans aangeduid als G_c en gegeven door de formule G_c = K_Ic²/E . Deze grootheid is dus af te leiden uit de kerftaaiheid en de elasticiteitsmodulus⁵. Een courante Nederlandse naam heeft G_c nog niet. De term taaiheid ligt voor de hand, maar wordt al gebruikt als alternatieve benaming voor breukrek. Wellicht dat we toughness kunnen vertalen als ‘stevigheid’?

Voor de volledigheid noemen we nog een andere af te leiden grootheid, te weten K_Ic/E. Deze geniet zelfs in het Engels geen naam maar heeft wel een concrete betekenis: het is namelijk een indicatie voor de maximale rek die een materiaal kan weerstaan alvorens, in aanwezigheid van een kerf met zekere vorm en lengte, bros te falen. Dit is relevant voor onderdelen zoals kliksluitingen, waarbij het materiaal herhaaldelijk een forse vervorming te verduren krijgt.

Mechanische eigenschappen van diverse materialen.

Tabel 1 zet de genoemde eigenschappen voor diverse materialen op een rij. Merk op hoe goed het bekende 18/10 RVS het doet: het is niet alleen roestvast, maar kan ook beslist tegen een stootje. In het algemeen scoren constructiemetalen hoog op kerftaaiheid en toughness (= stevigheid?), en redelijk op K_Ic/E . De kerflengtes a_c waaronder nog van taaie breuk sprake is, zijn voor metalen ook aanzienlijk. Het is derhalve zeker relevant om naar de specifieke elastische energie-opname W_el  te kijken, en ook daarop scoren de metalen opnieuw goed.

Kunststoffen hebben, vergeleken met metalen, een geringe kerftaaiheid en toughness, maar juist hoge waardes voor K_Ic/E . Qua W_el scoren kunststoffen verrassend goed, maar pas op: zelfs kleine kerfjes brengen ons al in het gevaarlijke brosse faalgebied, en dan is die grootheid niet meer van toepassing. Hebt u een kras in uw veiligheidsbril of in het vizier van uw motorhelm? Tijd voor een nieuwe – nu weet u waarom! Baksteen tenslotte scoort op alle fronten slecht, net als alle (technisch) keramiek. De argwaan van constructeurs voor deze materialen is dus terecht.

Slagvastheid

Wie bekend is met slagvastheid, kent ook de termen Charpy en Izod. Beide verwijzen naar tests om de slagvastheid van materialen te meten. Dit gebeurt zeer pragmatisch, middels een pendule die als valhamer fungeert⁶. Er worden proefstukken met en zonder V-vormige kerf getest; in het eerste geval valt er een correlatie te verwachten met de kerftaaiheid en/of toughness van het materiaal in kwestie, in het tweede met de specifieke energieopname.

Typerend voor de tests zijn de relatief hoge reksnelheden die erbij optreden. Dat verschilt van trekproeven en tests op kerftaaiheid, die quasi-statisch worden uitgevoerd. Vooral voor kunststoffen is dit relevant, want bij deze materialen zijn vloeigrens en elasticiteitsmodulus significant afhankelijk van de reksnelheid. Deze afhankelijkheid is ook wat deze materialen gevoelig maakt voor kruip en relaxatie, maar dan bij zeer korte in plaats van zeer lange tijdsschalen. De genoemde correlaties zijn, althans voor kunststoffen, dan ook niet sterk.

Kunnen deze valhamertests ons een objectieve, absolute maat opleveren voor de ‘stevigheid’, als materiaaleigenschap? Het antwoord is eenduidig: nee. Zowel bij Charpy- als Izod-tests hangen de resultaten daarvoor te sterk af van grootte en vorm van het proefstuk. We kunnen deze tests wel gebruiken om te bepalen bij welke temperatuur een materiaal een eventuele bros-taai transitie vertoont: zo waren het Charpy-tests die uitsluitsel gaven over het mysterieuze en desastreuze brosse falen van de Liberty Ships in WOII. Beide tests worden ook ingezet om materialen onderling te vergelijken op slagvastheid, als relatieve tests, maar een echte materiaaleigenschap bepalen ze niet.

ABS, PC, PP of TPU?

Het voorgaande wijst erop dat stevigheid, althans bij kunststoffen, in ieder geval iets te maken heeft met kerftaaiheid en/of toughness. Laten we daarom eens enkele kunststoffen vergelijken op deze eigenschappen, te weten acrylo-butadieen-styreen (ABS), polycarbonaat (PC), polypropyleen (PP) en thermoplastisch polyurethaan (TPU).

.

Wat is ‘de stevigste’ kunststof (brosse breuk)? Bron: Cambridge Engineering Selector

Afbeelding 2 toont het resultaat. Hier zijn bewust ‘grades’ gekozen die voor een spuitgietdeel kunnen worden ingezet waarbij robuustheid van belang is – vandaar ‘high impact’. De conclusie is duidelijk: TPU wint het zelfs van PC, en dat zal voor velen een verrassende uitkomst zijn. Er is ook nog een ‘low impact grade’ van polysytreen (PS)  meegenomen en dit toont dat er op de gekozen eigenschappen veel te winnen en te verliezen is.

Afbeelding 2 heeft betrekking op situaties waarin brosse breuk aan de orde is, dan wel vermeden moet worden. Wanneer we naar taaie breuk zouden kijken dan komen de specifieke (elastische) energieopname W_el en – uitsluitend voor vergelijkende tests – de slagvastheid in beeld. Op deze eigenschappen komt PC als winnaar naar voren, maar nu lijkt TPU een goede tweede. We kunnen hieraan nog toevoegen dat TPU slechts een enkel lid is van grote familie van polyurethanen. Met thermohardend PU zijn vaak nog betere resultaten haalbaar. De inzet belicht enkele verrassende productieprocessen voor deze materialen.

Pleidooi voor stevigheid

"Stevigheid is geen materiaaleigenschap!", zo doceert menig materiaalkundedocent. Maar intussen werken constructeurs graag met stevige materialen – en anders vragen kun klanten er wel om. Aan wat we met ‘een stevig materiaal’ bedoelen is wel degelijk objectief en kwantitatief invulling te geven. De Engelse materiaaleigenschap toughness lijkt een goede kandidaat om voor deze invulling te zorgen . Dit is ook een echte materiaaleigenschap, en is dus onafhankelijk van vorm en grootte van het proefstuk te bepalen. In de praktijk zal het uiteraard nog steeds lastig blijken om de rollen van materiaal en vorm te scheiden, net zoals mensen vaak moeite hebben om bijvoorbeeld elasticiteit los te zien van de dikte van een balk of plaat. Echter, materiaalkundig gezien lijkt er geen reden om het begrip stevigheid uit de weg te blijven gaan.

http://www.eriktempelman.com/

** voetnoten

¹ De K_Ic doelt op trekspanning dwars op de kerf; voor afschuiving zijn er K_IIc en K_IIIc .

² Vermoeiingsscheuren zijn ook kerfjes, en kerftaaiheid correleert dan ook met vermoeiingssterkte. De relatie is echter complex, en het is verstandig om voor ogen te houden dat kerftaaiheid betrekking heeft op statisch falen en niet op dynamisch falen, zoals bij vermoeiing het geval is.

³ Bij koudbrosheid bijvoorbeeld ligt dit anders: dan faalt staal wel degelijk als gevolg van een tekort aan kerftaaiheid!

⁴ Een volledige afleiding valt buiten het bestek van dit artikel. Aanbevolen wordt Materials van Ashby et.al. 3^e editie, Elsevier 2013.

⁵ Het is verwarrend dat de materiaalkunde de letter G ook gebruikt voor de glijdingsmodulus. Als alternatief voor G_c komt men ook wel γ_woc tegen, met woc als afkorting van work-of-fracture.

⁶ Details van deze tests, zie ISO 179 (Charpy) en ASTM D256, D4812 en ISO 180 (Izod)