Ouderwets de 21e eeuw in: spaceframes

Door Erik Tempelman, adviesbureau eriktempelman.com, universitair hoofddocent TU Delft – Industrieel Ontwerpen 

Torenkranen zijn een ander voorbeeld van vakwerkconstructies; de frames voor matrixborden over de snelweg zijn nog een derde. Ook bij deze constructies springen moderniteit of esthetiek niet bepaald in het oog. Afbeelding 1 brengt de bouwkundige treurigheid voor u in beeld. We hebben er gelijk één van ‘s werelds mooiste auto’s bijgezet, die onder zijn verleidelijk glimmende plaatwerk ook weer zo’n oersaai en spuuglelijk vakwerk blijkt te hebben, de legendarische Mercedes 300 SL. Het verschil tussen carrosserie en frame is als dag en nacht.

Terecht is dat negatieve imago natuurlijk niet. Vakwerken zijn voor dit soort constructies nu eenmaal de beste oplossing, net zoals diezelfde kakkerlak en krokodil evolutionair gezien amper te verbeteren zijn. Deze bijdrage belicht waarom. En, vakwerken kunnen wel degelijk een bijzondere ‘look’ krijgen, waar prijs noch efficiency onder hoeft te leiden. Kunstenaar Kenneth Snelson heeft hiervan met zijn ‘needle towers’ (zie afbeelding 2) al een intrigerende voorzet gegeven. Laten we om de rehabilitatie te beginnen vanaf nu een meer aansprekende term gebruiken: aangezien een vakwerk een frame is dat de ruimte opzoekt, kiezen we voor ‘spaceframe’.

Afbeelding 2 Een van Snelsons ‘needle towers’. (Foto: Clayton Shonkwiler (CC BY.2.0)) 

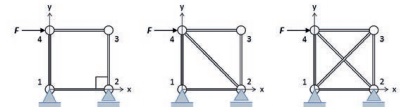Afbeelding 3 Types van spaceframes. 

Types van spaceframes

Achter de veelvormigheid van spaceframes schuilt een simpel systeem, dat in afbeelding 3 uit de doeken wordt gedaan. We werken hier vooralsnog in het platte vlak (een ‘vlakwerk’ dus, als u wilt); de 3D-varianten komen zo dadelijk. U ziet drie frames, elk bestaande uit vier knooppunten en verbonden door een aantal staven: vier staven in frame (a), vijf in frame (b) en zes in frame (c). Merkt u op dat het frame (a) één star knooppunt heeft dat zowel krachten als buigende momenten kan doorgeleiden; alle andere knooppunten zijn scharnieren en geleiden alleen krachten door. Verder zijn de twee diagonale staven in afbeelding (c) in het midden niet met elkaar verbonden. De externe belasting is steeds een enkele kracht op knooppunt 4, de verbinding met de vaste wereld gaat via knooppunt 1 en 2. Voor de typering doet dat niet ter zake, maar het helpt om een specifiek voorbeeld te geven.

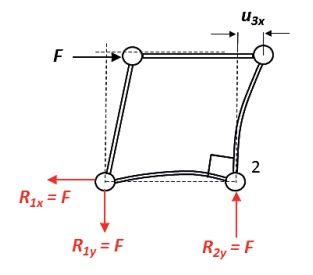Afbeelding 4 Frame (a) met zijn vervormingen. 

Hoe voert elk frame de belasting door naar de vaste wereld? Wel, in frame (a) gaat dat gepaard met buiging en dus met relatief grote vervormingen: Afbeelding 4 laat dit (overdreven)zien, samen met de resulterende reactiekrachten, weergegeven in rood. Punt 3 verschuift een aanzienlijke afstand naar rechts: dit is de u_3x in het plaatje. In frame (b) treedt geen buiging op: hier zijn alleen trek- en drukkrachten aan het werk. Dat maakt dit frame zeer veel1 efficiënter dan frame (a): al die ouderwets aandoende ‘driehoekjes’ zijn beslist van nut! Maar als er ook maar één staaf bezwijkt, bijvoorbeeld door uit te knikken, dan wordt frame (b) een mechanisme en is het gedaan met de constructie. Wat dat aangaat biedt frame (c) enige extra veiligheid, want hier kan in principe wel een staaf bezwijken voordat het frame als geheel het begeeft.

Staat u alstublieft even stil bij de absolute grootte van de vervormingen. Een frame kunnen we in principe belasten totdat er ergens in het materiaal de vloeigrens wordt bereikt – ervan uitgaande dat knik afdoende wordt voorkomen, wat doorgaans betekent dat op druk belaste staven niet te lang mogen zijn. Voor belasting op trek en druk, zoals in frames (b) en (c), kunnen we de Wet van Hooke er dan weer eens bij pakken, dus σ = E·ε. Bij metalen frames van deze types zijn de bijbehorende rekken dan maximaal enkele tienden van procenten: een metersgroot frame vervormt dus slechts millimeters. [We blijven doorgaans ruim onder de vloeigrens. De rekken en vervormingen zijn dan dus nog kleiner.] Bij frame (a) is dit totaal anders: hier zijn de vervormingen zeer veel groter. Waar buiging is, is grote vervorming!

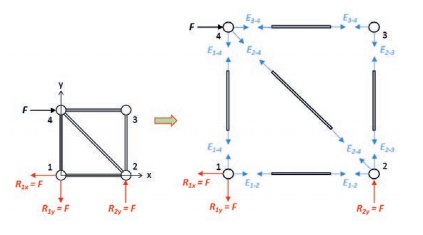Afbeelding 5 Frame (b) uit afbeelding 3 nader geanalyseerd. 

Nadere analyse: weer die statica

Wanneer hebben we genoeg staven om buiging te voorkomen ten faveure van trek- en drukkrachten? Deze vraag kunnen we beantwoorden met behulp van de statica – u weet nog wel: dat onpopulaire basisvak van toen. Elk knooppunt heeft, voor een 2D spaceframe, twee graden van vrijheid, en voor N knooppunten kunnen we dus 2N evenwichtsvergelijkingen opstellen. Hiervan hebben we er drie nodig om de reacties mee te bepalen, uitgaande van statisch bepaald opgelegde frames. De overblijvende 2N – 3 vergelijkingen leveren ons dan de staafkrachten: met de N = 4 uit Afbeelding 3 hebben we vijf vergelijkingen over en dat is precies het aantal staven in frame (b): dit frame kunnen we derhalve beschouwen als statisch bepaald. Zulke frames zijn simpel door te rekenen, bijvoorbeeld met de zogeheten ‘knooppuntsmethode’. Afbeelding 5 toont deze aanpak. We vinden dat E1-2 = F, E2-3 = E3-4 = 0, E3-4 = F en E2-4 = – √2F. Merk op dat de oplossing uniek is: bij zo’n frame is er maar één manier waarop de externe belasting (de ‘actie’) door het frame naar de vaste wereld wordt geleid (de ‘reactie’). En ja, in dit geval zouden we zelfs die twee ‘nul-staven’ (dat wil zeggen: staven zonder belasting) weg kunnen halen, maar dat zou anders kunnen zijn als de actie op een ander knooppunt aan zou grijpen. U begrijpt het idee.

Voor frames van type (c) komen we minstens één evenwichtsvergelijking tekort. Ditzelfde probleem komt naar boven als we in het getoonde frame (a) meer dan één knooppunt star zouden maken. In beide gevallen hebben we te maken met een statisch onbepaald spaceframe. [Frame (a) is, interessant genoeg, ook statisch bepaald: zie verder in ‘NSFD – engineering essays on structures & materials’, E. Tempelman, Boekengilde 2020.] Dan zijn er in theorie eindeloos veel manieren waarop de belasting kan worden doorgeleid – maar wat is de juiste? Een zogeheten ‘constitutieve vergelijking’ biedt een uitweg: dit is een expliciete relatie tussen kracht en vervorming, zoals de Wet van Hooke voor trek en druk, of een vergeet-me-nietje voor buiging. Met die extra vergelijking kunt u in beginsel aan de slag. In de praktijk is dat echter niet eenvoudig en verdient het gebruik van computers beslist de voorkeur. De daarop draaiende software gebruikt overigens ook zulke constitutieve vergelijkingen, maar dat terzijde. Als derde optie heeft u vandaag de dag ook handige appjes, zoals Framedesign (ontwikkeld door onze landgenoot Martinus van de Ruitenbeek), waarmee het snel en makkelijk rekenen is. Aanrader!

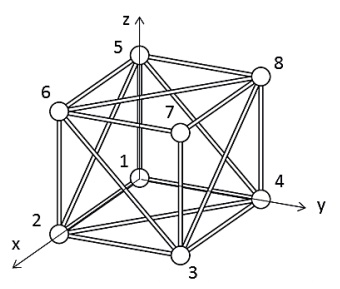Afbeelding 6 Een kubusvormig 3D-type (b) spaceframe. 

Voordat we de praktijk er bij pakken nog twee (eigen)aardigheden. Primo: werkt u in 3D, dan heeft elk knooppunt niet twee maar drie graden van vrijheid. Statische oplegging vraagt nu niet drie maar zes onafhankelijke reacties, en de typerende vergelijking is nu niet 2N – 3 maar 3N – 6. Een kubusvorming spaceframe, dus met N = 8 knooppunten, moet dan precies 18 staven hebben om statisch bepaald te zijn, dat wil zeggen: van type (b). En dat moeten dan onafhankelijke staven zijn: elk vlak van de kubus moet precies één keer worden ‘uitgekruist’. Afbeelding 6 laat zien waar dat toe leidt.

Secundo: zowel externe belastingen als reactiekrachten moeten netjes op knooppunten aangrijpen, en niet ergens dwars op een staaf tussen de knopen – dat laatste leidt onherroepelijk tot buiging en groot verlies van efficiency. Dezelfde voorwaarde geldt uiteraard ook in 2D. Spaceframes moeten dus niet alleen correct worden ontworpen maar ook correct worden gebruikt.

De praktijk van spaceframes

Wie daadwerkelijk aan het rekenen gaat, ontdekt al snel dat die efficiënte spaceframes van type (b), evenals hun statisch onbepaalde broeders van type (c), inderdaad enorme belastingen aankunnen – als de sommetjes kloppen. In de praktijk rekent u zich doorgaans echter onterecht rijk. Een voorbeeld: worden belastingen herhaaldelijk aangebracht, casu quo is er sprake van vermoeiing, dan moeten we bij trekstaven niet onder de vloeigrens blijven maar onder de (doorgaans fors lagere) vermoeiingssterkte, én moeten we terdege rekening houden met spanningsconcentraties. We benoemden dit probleem al eerder in NSFD – IV: belastingsvormen. En bij drukstaven zorgt de beroemende Euler-knikvergelijking voor een danige overschatting van wat de praktijk vermag: knik treedt doorgaans beduidend sneller op dan zelfs de geniale Euler voorzag, hetgeen ook al eerder werd gemeld.

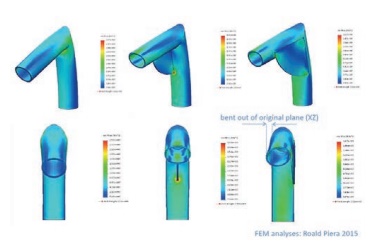Afbeelding 7 Secundaire buiging als gevolg van een asymmetrisch versterkt knooppunt. (Roald Piera) 

Extra punt van aandacht hierbij is ‘secundaire buiging’. Om dit verschijnsel te illustreren, keren we terug naar dat ene starre knooppunt uit frame (a). Ziet u afbeelding 7, waar drie varianten van deze knoop zijn weergegeven, bovenaan in isometrisch aanzicht, onderaan als gezien in het vlak van de constructie. Uiterst rechts ziet u het onbedoelde gevolg van de asymmetrisch aangebrachte versterkingsplaat: de bovenste staaf buigt uit het vlak. Voor de knikbestendigheid is dit welhaast een ‘schot in de buik’. Secundaire buiging treedt altijd op, ook in frames van types (b) en (c), als de hartlijnen van de staven effectief niet door één punt lopen. [Er is nog een probleem met de in de rechterafbeelding aangegeven versterkende ‘schetsplaat’. Bij buiging wordt de neutrale lijn van de betreffende balk hoegenaamd niet belast. De schetsplaat zit precies op die neutrale lijn… en dit onderdeel draagt dus amper belasting, zoals ook uit de kleuren blijkt.]

Ondanks deze kanttekeningen zijn spaceframes nog steeds ijzersterk, mits we de negatieve effecten van knik, buiging en (in 3D) torsie buiten de deur weten te houden. Voor de eerder genoemde drie voorbeelden – mast, kraan, frame – is de goede winddoorlatendheid ook van belang, evenals de lage kosten: staal is goedkoop en makkelijk te verkrijgen, verwerken en verbinden. Los daarvan bieden spaceframes nog een ander, vaak doorslaggevend voordeel: lage investeringen! Dat was de reden waarom Mercedes indertijd voor hun 300 SL een spaceframe koos. Bij de geplande kleine aantallen van deze sportauto was een zelfdragende carrosserie uit gestampte staalplaten volstrekt onhaalbaar. Aardig detail is dat ‘Das Haus’ ervoor koos om de coupé en cabrio nagenoeg hetzelfde frame te geven. Om voldoende overall torsiestijfheid te hebben, had dit frame veel bouwhoogte nodig. Dat leidde tot hoge dorpels – en in deze lage auto vroeg dat op zijn beurt om de karakteristieke vleugeldeuren voor de coupé… een sterk staaltje van form follows structure. Ziet u wel: spaceframes zijn cool.

Post scriptum

De vormvrijheid van 3D printen stelt ons tegenwoordig in staat om ogenschijnlijk massieve constructiedelen ‘uit te hollen’. Het materiaal wordt zodoende een constructie… een spaceframe-constructie, om precies te zijn! Afbeelding 8 geeft hiervan een indruk.

Afbeelding 8 Een ge3Dprint onderdeel (‘spider bracket’). Materiaal wordt constructie – en omgekeerd. (Foto: Renishaw)

Dit artikel verscheen in Constructeur 6/7 – 2020