(Not) safe for designers? I – Statica

Door: Erik Tempelman, adviesbureau eriktempelman.com , universitair hoofddocent TU Delft – industrieel ontwerpen

Wie aan een constructie wil rekenen heeft dit beeld beslist nodig. Daarnaast biedt statica een uitstekende gelegenheid om te leren denken als een ingenieur. Deze eerste bijdrage onder de noemer (Not) Safe For Designers?, het begin van een serie over constructies en materialen, is dan ook gewijd aan een rehabilitatie van dit ondergewaardeerde basisvak. Heeft u een andere achtergrond? Geen paniek: de essentie van de statica volgt hieronder. Werktuigbouwers c.s. zullen dit alles ongetwijfeld herkennen – en hopelijk opnieuw leren waarderen. En mocht u statica doceren, dan vindt u hier wellicht nieuw materiaal voor uw eigen lesprogramma.

Constructiedeel

In de statica beschouwen we een constructiedeel aanvankelijk als een star lichaam, dat de erop aangrijpende belastingen – ook wel acties genaamd – zonder te vervormen doorvoert naar de punten waar het aan de ‘vaste wereld’ verbonden is. Wat precies die vaste wereld is, hangt af van het constructiedeel in kwestie: een draagarm van een wielophanging zit bijvoorbeeld vast tussen wiel en chassis, een keukentrap zit ‘vast’ tussen u en de vloer, enzovoorts. Deze punten, hetzij inklemmingen, hetzij opleggingen, worden hierbij gemodelleerd als reacties en zodoende wordt het constructiedeel vrijgemaakt. Als het aantal reacties gelijk is aan het aantal vrijheidsgraden van het constructiedeel, dan spreken we van een statisch bepaald probleem. [Aanvullende eis: de reacties moeten onafhankelijk van elkaar zijn. Bij bijvoorbeeld drie rollende opleggingen, elk dezelfde kant op rollend, is dit niet het geval.] We kunnen de reacties dan eenvoudig vinden; gegeven een specifieke situatie vormen de reacties gezamenlijk bovendien een unieke oplossing op ons probleem. Er is dan feitelijk maar één manier waarop de acties via de constructie naar de vaste wereld kunnen worden geleid. Het zo begeerde beeld van acties en reacties is dan dus makkelijk en ondubbelzinnig te bepalen.

Voorbeeld

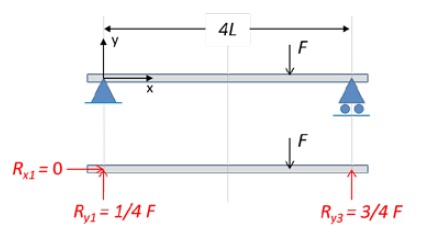
Tijd voor een voorbeeld: zie het balkje in afbeelding 1 (boven), waarbij de bevestiging met de vaste wereld is gemodelleerd als een combinatie van een zogeheten vaste oplegging (links) en een rollende op legging (rechts). We vatten hierbij het balkje, dat in het echt natuurlijk een driedimensionaal object is, op als werkend in het platte vlak, ofwel in ‘2D’ zodat het niet zes maar slechts drie vrijheidsgraden bezit. En in dit geval zijn er ook precies drie reacties: twee links (te weten: R_x1 en R_y1) en één rechts (genaamd R_y3 – u ziet zo dadelijk waarom). Als er op de balk nu een enkele kracht F aangrijpt zoals geschetst, dan moeten de reacties zijn zoals aangegeven in afbeelding 1 (onder) – anders is er geen statisch evenwicht van krachten en momenten. Of u deze oplossing nu vindt door ‘trial-and-error’ of door systematisch vergelijkingen op te lossen, compleet met zorgvuldig beredeneerde tekenafspraken, maakt niet uit: de oplossing is uniek, dus als hij voldoet is het automatisch de juiste.

Nu worden constructiedelen doorgaans zodanig aan de vaste wereld bevestigd dat er meer reacties dan vrijheidsgraden zijn: we hebben dan te maken met een statisch overbepaald probleem. [Ook wel ‘statisch onbepaald’ genoemd, al is dat technisch niet geheel correct.] Dan zijn er in principe oneindig veel oplossingen mogelijk en is het pad van actie naar vaste wereld niet eenduidig. Om dé oplossing te vinden, moeten we ofwel aannemen dat de opleggingen en inklemmingen vervormen, ofwel dat het constructiedeel zelf vervormt en dus niet star is.

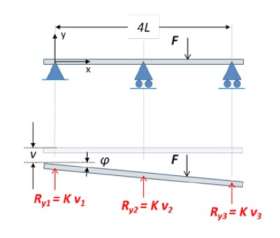Afbeelding 2. Een statisch onbepaalde constructie; de verende-opleggingaanpak 

Nog een voorbeeld

Opnieuw een voorbeeld: zie afbeelding 2. Dit is dezelfde balk als eerst, met dezelfde actie F, maar nu met een derde oplegging en wel in het midden. Om de reacties te vinden, kunnen we aannemen dat de drie opleggingen elk een zekere afstand in gaan veren, elk met veerconstante K. Als de balk zelf zich star gedraagt, dan kunnen we deze afstanden v₁, v₂ en v₃ uitdrukken in de verplaatsing van de oorsprong v, de hoekverdraaiing van de balk φ, en de gegeven lengte L. De onbekende veerconstante K valt verder uit de vergelijkingen weg en dat is logisch: deze ‘truc’ moet immers werken met stijve of slappe veren. [Mits de hoek φ niet te groot wordt, zodat we gebruik kunnen maken van de versimpeling tan(φ) = φ.] We houden dus twee onbekenden over en hebben ook twee evenwichtsvergelijkingen ter beschikking, te weten die voor verticaal krachtenevenwicht en die voor evenwicht van momenten om een willekeurig punt. [Er is nog een derde evenwichtsvergelijking, te weten die voor het horizontaal krachtenevenwicht. Deze vertelt ons dat, in afwezigheid van externe belastingen in die richting, de reactie Rx1 gelijk is aan nul.] We komen uit op de reacties:
– R_y1 = F/12
– R_y2 = 4F/12
– R_y3 = 7F/12

Rekent u het maar even na. We hebben overigens de vierde reactie (dat wil zeggen R_x1) uit het plaatje weggelaten, dit voor de duidelijkheid. In eerste benadering is deze gelijk aan nul, maar als de hoek φ relatief groot wordt, dan is dat niet langer het geval: de balk schuift dan naar rechts.

Crux

Is dit nu dé oplossing? Nee. Ditzelfde probleem kunnen we namelijk ook aanpakken door aan te nemen dat de balk vervormt en dat de opleggingen star blijven. Dit scenario is geschetst in afbeelding 3.
 

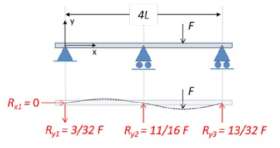Afbeelding 3. Een statisch onbepaalde constructie; de buigende-balk-aanpak. 

Met enig slim gebruik van de vergeet-me-nietjes voor buigende balken komen we dan ook op dé oplossing – en deze is duidelijk anders dan degene die we eerder bepaalden! [Er zijn tegenwoordig handige apps voor uw smartphone om dit soort situaties mee door te rekenen. Zoekt u maar eens in de app store naar beam HPC van Kurt Gramoll. aanrader!] De verklaring is even eenvoudig als belangrijk: het is niet hetzelfde probleem. Afhankelijk van wat er precies vervormt, en hoe, kiest de belasting een andere weg naar de vaste wereld.

En dat brengt ons op de crux van de statica. Die zit namelijk helemaal niet in het correct oplossen van vergelijkingen, maar (zoals zo vaak…) in het correct opstellen ervan. Om dat te doen, moeten we eerst goed bepalen waarmee we precies te maken hebben. Een forse stalen balk, rustend op drie rubber blokken, zal zich gedragen zoals in afbeelding 2, maar een dun houten latje op en stijve ondersteuning doet wat we in afbeelding 3 zagen. En wie weet hebben we te maken met een mengvorm en moeten we beide soorten vervorming meenemen teneinde een betrouwbaar model van de situatie te maken en het gewenste complete krachtenbeeld te verhelderen.

Nog interessanter

Denkt u nu nog eens terug aan uw opleiding: is dit punt toen afdoende onder uw aandacht gebracht, of lag het accent vooral op het oplossen van voorgekookte (en het moet gezegd, overwegend statisch bepaalde) problemen? Tsja, dan wordt het vanzelf saai natuurlijk – u kunt net zo goed sudoku’s gaan oplossen.

Het wordt nog interessanter als we ons realiseren dat die opleggingen en inklemmingen op hun beurt ook modellen zijn. Echte bevestigingspunten conformeren zich vaak slechts met frisse tegenzin aan het ideaalbeeld dat het ‘handboek statica’ voor ogen heeft. Kijkt u eens naar de boekenplank in afbeelding 4 en naar de twee zeer verschillende wijzen waarop deze (opnieuw in ‘2D’) kan worden gemodelleerd.

Afbeelding 4. Een boekenplank (boven) met twee verschillende odellen (onder) voor de bevestigingspunten. 

Wederom geldt dat niet het oplossen maar het opstellen van de vergelijkingen onze echte aandacht verdient. Opleggen of inklemmen? Misschien is het bij de echte constructie wel een mix van beide.
Mocht u twijfelen aan de relevantie, bedenkt u dan dat een ingeklemde balk bij dezelfde belasting minder zal doorbuigen dan wanneer deze balk opgelegd wordt. En hierbij staat de boekenplank uiteraard model voor tal van toepassingen – waaronder bijvoorbeeld de wielophanging van uw auto, of de treden van uw keukentrap.

Laatste woord

In de ogenschijnlijk oersaaie statica verschuilen zich dus enkele belangrijke lessen in modelmatig denken. De student leert bijvoorbeeld dat elk model weliswaar ‘fout’ is, maar dat een slim gemaakt model desondanks heel nuttig kan zijn. Daarnaast is de vaardigheid in het opstellen en oplossen van vergelijkingen altijd goed om te oefenen, en daarvoor kunt u bij de statica zeker terecht. Maar er is nog iets dat dit vak potentieel zo waardevol maakt en dat is dat we de oplossingen, althans in beginsel, ook kunnen bepalen door ze te meten.

In afbeelding 5 ziet u hoe dit in zijn werk kan gaan; meer dan een paar weegschalen, drie schuimrubber blokjes, een houten latje en een gewicht hebben we niet nodig om bijvoorbeeld het scenario uit afbeelding aan de praktijk te toetsen. Opbouwen, weegschalen op nul zetten, gewicht plaatsen, en wat de displays dan laten zien, moet corresponderen met hoe de krachten in dit geval verdeeld worden over de drie opleggingen. Voor wie de statica daadwerkelijk op deze wijze toetst, is er nóg een les te leren: dit soort testjes is namelijk nog niet zo eenvoudig uit te voeren als het wellicht lijkt. Maar ook dat is een prima les, want uiteindelijk heeft de werkelijkheid altijd het laatste woord.

Afbeelding 5. Het scenario van de verende oplegging, beproefd met een test. 

Bron: Constructeur