Meetmethoden in de fotometrie

Fotometrie kan worden beschouwd als een moderne wetenschap: in 1924 slaagde de Commission Internationale de l’Eclairage (CIE) erin om de respons van een gemiddeld oog vast te leggen. De commissie mat de ogen van een aanzienlijke groep testpersonen, en bracht de data samen in de fotopische curve.

De fotopische curve is te zien in figuur 1. Uit de curve blijkt dat de mens het sterkst reageert op de kleur groen en minder gevoelig is voor de spectrale uitersten, rood en violet.

In de fotometrie zijn de volgende vier grootheden de belangrijkste:

• illuminantie;
• luminantie;
• lichtintensiteit;
• lichtstroom.

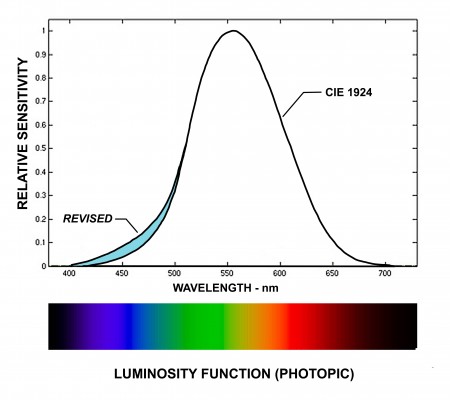
Figuur 1. CIE fotopische curve.

De basiscomponent van alle instrumenten voor het meten van licht is een omvormer die licht omzet in een meetbaar elektrisch signaal dat kan worden versterkt. Voorbeelden in de volgorde van toenemende gevoeligheid hiervan zijn: een thermocel (thermozuil, bolometer), een fotovoltaïsche cel (selenium barrier-layer cell), een fotodiode (gewoonlijk silicium) of fotomultiplicator. Afhankelijk van het gewenste compromis tussen gevoeligheid, kostprijs, afmetingen en dergelijke kan een geschikte keuze worden gemaakt uit het bovenstaande.

Illuminantie (E, lux, lm/m2)

Illuminantiemeting is de meting van een hoeveelheid zichtbaar licht die op een bepaalde oppervlakte valt. In de metrische eenheden wordt een lumen per vierkante meter een zogenoemde lux (10,76 lux = 1 footcandle).

Illuminantie of verlichtingssterkte wordt uitgedrukt als de lichtstroom per oppervlakte-eenheid:

E = (dF / dA)

Illuminantiemeter (luxmeter)

Met illuminantie (lux) meters, is de omvormer die gebruikt wordt vaak een fotovoltaïsche cel of een fotodiode. De eerste combineert de voordelen van eenvoud, lage kostprijs, geen noodzaak van een elektrische voeding en een relatieve hoge gevoeligheid. Het nadeel van deze cel is het ontstaan van saturatie bij hoge lichtsterktes. De fotodiode wordt zeer vaak gebruikt vanwege zijn hoge gevoeligheid, snelheid en stabiliteit. Het nadeel is de behoefte aan een elektrische voeding.

Een luxmeter van hoge kwaliteit moet beschikken over de volgende eigenschappen:

• a. Accurate V(λ) correctie

Met de hulp van kleurfilters is de gevoeligheid van de cel aangepast aan de gevoeligheidscurve van het oog. Omdat deze correctie nooit perfect is, zullen er storingen optreden bij het meten van lichtbronnen met verschillende spectrale energiespreidingen en moet elke luxmeter vergezeld gaan van een tabel van correcties.

• b. Nauwkeurige correctie voor niet-loodrecht invallend licht (cosinus correctie)

Licht dat invalt op de cel bij een gegeven hoek ten opzichte van de normaal wordt geëvalueerd volgens E_α = (I_α cos(α)) / r². Het glasachtige oppervlak van de cel zal echter wat van het invallende licht reflecteren, hierdoor wordt de cel weer afhankelijk van de invalshoek. Bovendien zal bij een zeer grote instralingshoek de rand van de cel beschenen worden, wat screening veroorzaakt. Om te compenseren voor al deze effecten wordt de cel voorzien van een speciaal deksel met een diffuus materiaal.

• c. Ongevoeligheid voor de omgevingstemperatuur

Omdat de lichtgevoeligheid van een Si-diode enigszins temperatuurafhankelijk is, wordt een goede luxmeter voorzien van een thermostaat en verwarming om de fotodiode op een constante temperatuur te houden, boven de kamertemperatuur (bijvoorbeeld op 35 °C).

Ondanks de hoge kwaliteit van de verschillende componenten, lijden luxmeters aan veroudering. Een regelmatige (jaarlijkse) kalibratie is daarom noodzakelijk.

Luminantie (L, nit, cd/m2)

Ook bekend als fotometrische helderheid; luminantie is de maat voor de gereflecteerde of uitgezonden flux van een relatief vlak en uniform oppervlak. De techniek houdt rekening met de grootte van het gemeten oppervlak en de hoek tussen de opnemer en het oppervlak.

Luminantie kan worden gezien als lichtintensiteit per oppervlakte-eenheid en wordt in metrische termen uitgedrukt in candela per vierkante meter.

Luminantie wordt gedefinieerd als de lichtintensiteit per eenheid van zichtbare oppervlakte:

L = (dI / dAcos(a))

Luminantiemeter

Om helderheid te meten, moet het gezichtsveld van de detector worden beperkt, en de hoek berekend. Gewoonlijk wordt een lens of keerschot hiervoor gebruikt. In feite functioneert het menselijk oog, met een lens en diafragma, als een luminantiemeter.

Het hart van de luminiantiemeter is niets meer dan een luxmeter, die omwille van de gewenste hoge gevoeligheid, meestal een fotomultiplicator als detector heeft.

Een focuslens dient om het meetgebied te beperken op de meetcel. Om de meetrichting en de meetafstand te kunnen bepalen, wordt een deel van de invallende lichtbundel onderschept door een half doorlatende spiegel of bundelsplitser en doorgegeven aan het oculair. Er is meestal een variabel diafragma aan de voorzijde van de meetcel, zodat de acceptatiehoek en/of vorm van het meetoppervlak kan worden ingesteld. Als de meetafstand voldoende groot is ten opzichte van de focuslengte van de lens, kan worden aangetoond dat:

L = E_d (4f² / πd²)

waarbij:

E_d = illuminantie op het diafragma

d = diameter van de lens

f = focuslengte van de lens

In deze vergelijking is de meetafstand niet weergegeven. Hierdoor is, mits de luminantie constant is over het meetoppervlak, de gemeten luminantie onafhankelijk van de afstand tussen de detector en de meetvlakken. Dat komt omdat veldgrootte en bronsterkte verschillen in directe verhouding tot elkaar als functie van de afstand.

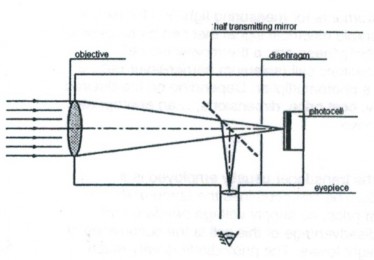
Figuur 2. Werkingsprincipe van een luminantiemeter

Lichtintensiteit (I, candela, cd)

Lichtintensiteit is een grootheid waarbij de bronrichting en divergentie in het spel komen. Het wordt gedefinieerd als de hoeveelheid lichtstroom uniform uitgestraald in een ruimtehoek. De basiseenheid van lichtsterkte is de candela, gelijk aan één lumen per steradiaal. Om de lichtsterkte te berekenen, dient de lichtstroom gedeeld te worden door ruimtehoek:

I = (dF / dw)

De ruimtehoek (dω) is de openingshoek in het midden van een bol met een gebied op zijn oppervlak numeriek gelijk aan het kwadraat van de straal. De ruimtehoek is de verhouding van de boloppervlakte tot een ingesloten kegel, uit het midden van de bol tot de totale boloppervlakte.

Verschillende dingen worden duidelijk door deze definitie. Ten eerste is deze meting niet voor gecollimeerde lichtbronnen. Ten tweede is het onjuist voor niet-uniforme emitters. Om de lichtintensiteit te berekenen moet de oppervlakte van de detector (of de opening in het diafragma ervoor) en de afstand tot de lichtbron bekend zijn. Hieruit kan de ruimtehoek worden berekend en vervolgens worden verdeeld in de lichtroom uitlezing.

Lichtintensiteitmeter (goniofotometer)

Een specifieke lichtintensiteitmeter bestaat niet, of tenminste niet in een gemakkelijk bruikbare vorm. Gezien de relatie E = I/r², dus I = Er², is het duidelijk dat als een aantal eenvoudige maatregelen worden genomen elke luxmeter als een lichtintensiteitmeter kan worden gebruikt.

Goniofotometer.

Lichtsterktemetingen worden doorgaans niet uitgevoerd in een bepaalde richting. Het is meer een kwestie van het bepalen van de totale ruimtelijke lichtsterkteverdeling van de lichtbron. Een dergelijke meting kan worden uitgevoerd door een luxmeter op een cirkel rond de lichtbron te bewegen op voldoende afstand daarvan (minimaal 5 … 10 maal de afmetingen van de lichtbron). Natuurlijk kan dit resulteren in een zeer grote meetopstelling en daarom wordt in de praktijk een vaste positie voor de meetcel gekozen. Een schematische voorstelling van een dergelijke opstelling is weergegeven in figuur 3.

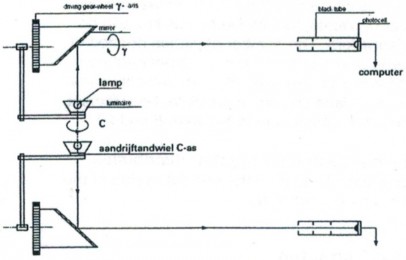
Figuur 3. Werkingsprincipe van een lichtdistributiemeter.

Een spiegel die is ingesteld op 45° richt het licht van de gemeten lichtbron naar de meetcel. De spiegel roteert om de horizontale as door de cilinder waarop deze is gemonteerd, terwijl de lamp beweegt in een cirkelvormige baan loodrecht op deze as. Gelijktijdig wordt de lichtverdeling in het meridiaanvlak gemeten en de lamp wordt over een bepaalde hoek in het horizontale vlak gedraaid. Daarna wordt het volgende vlak gemeten. Figuur 4 toont een voorbeeld van een meetresultaat.

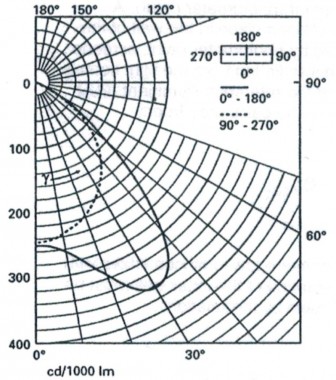
Figuur 4. Een voorbeeld van een lichtdistributie diagram.

Lichtstroom (Φ, lumen, lm)

Lichtstroom is de fundamentele eenheid van de fotometrie en wordt uitgedrukt in lumen. Het is een meting van de totale optische straling van een zichtbare lichtbron. Lichtstroom wordt berekend als de uitgestraalde hoeveelheid licht per tijdseenheid, gecorrigeerd voor de spectrale gevoeligheid van het menselijk oog, ofwel de som van de straling in het gebied  380 … 780 nm, afgewogen tegen de ooggevoeligheidskromme.

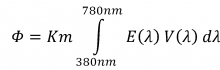
Waarbij

K_m:  constante (voor fotopisch zicht 683 lm/W)

V(λ): ooggevoeligheidfunctie

E(λ): stralingsstroom (W)

λ: golflengte

Lichtstroommeter

Er is geen speciale, gemakkelijk te gebruiken instrument voor het meten van de lichtstroom. In de praktijk worden de volgende meetmethoden aanvaard:

• a. Berekening van de lichtsterkteverdeling

Mits de lichtspreiding wordt gemeten over een voldoende aantal vlakken, kan de totale lichtstroom worden berekend. Het aantal vlakken dat nodig is om een hoge nauwkeurigheid te verkrijgen is sterk afhankelijk van het type van de lichtbron. Voor een rotatiesymmetrische bron zou het meten van 1 vlak in principe voldoende zijn. Hoewel in de praktijk het aantal varieert tussen 8 en 20.

• b. Berekening van de spectrale energie-stroomverdeling

Volgens de formule voor de lichtstroom, kan deze worden berekend uit een integraal van de absolute waarde van de energiestroomverdeling. Voorwaarde is natuurlijk de beschikbaarheid van een accurate, geijkte stralingsmeter. Voor het meten van lichtbronnen met een smalband spectrum moet de resolutie van de spectrofotometer voldoende hoog zijn (<1 nm).

• c. Meting met behulp van de Ulbricht (integratie) bol

Dit is de meest gebruikelijke manier voor het bepalen van de lichtstroom van een lichtbron. De te meten lichtbron is opgehangen in het midden van een bol, de binnenzijde van de bol is bedekt met een laag sterk reflecterende matte witte verf (fotometerverf). Een luxmeter wordt bij elke gewenste plaats in de wand van de bol bevestigd. Een plaat, eveneens voorzien van fotometerverf, schermt de meetcel af van directe straling van de lichtbron. Door het kennen van de lichtstroom van de referentielichtbron (Φ_ref), kan de lichtstroom van de testbron (Φ_x) worden berekend:

F_x = (E_x / E_ref) F_ref

Om in staat te zijn om ook lage lichtstomen nauwkeurig te meten, is het van belang dat de reflectie van de binnenwand zo hoog mogelijk is. Dit blijkt uit volgende relatie:

Ew = (Φ / 4pR²)(1 – ρ)^-1

Waarbij:
E_w: illuminatie op de wand van de bol
Φ: lichtstroom aanwezig in de bol
R: diameter van de bol
ρ: reflectie van de bolwand

Een voorbeeld, bij ρ = 0,8 is de ‘versterkingsfactor’ 1/(1- ρ) gelijk aan 5, bij ρ = 0,9 is dit al gestegen naar 10. Als de vorm en afmetingen van de test bron afwijken van de referentielamp, kan de zelfabsorptie van beide lampen verschillen. Met andere woorden, de meting door de luxmeter is niet altijd lineair evenredig met de geïnstalleerde lichtstroom.

Om deze verschillen in zelfabsorptie te bepalen, wordt een ‘witness lamp’ in de vorm van een kleine lichtbron gemonteerd op de wand van de bol. Met deze lamp ingeschakeld, wordt de luxmeter gelezen, zowel met de referentielamp en de testlamp in de meetpositie. De verhouding van deze twee waarden is de factor waarmee de testlamp moet worden gecorrigeerd.

Ulbricht bol 

Conclusie

Om voor visueel comfort te ontwerpen, is het noodzakelijk om de betekenis te begrijpen van de verschillende lichtparameters en hoe deze worden gemeten. In dit artikel zijn de meetmethoden voor de basis lichtgrootheden beschreven. Echter, lichtmeettechniek kan nog veel verder verdiept worden en de hier gepresenteerde informatie is dan ook de top van de ijsberg. Bovendien gaan enkele even zo belangrijke aspecten van lichtmetingen, zoals metingen en communicatie van kleur, verder dan de scope van dit artikel.

Om hier meer over te leren, bezoek dan het LED Event 2015 (2 december in België en 3 december in Nederland). De auteur van dit artikel zal daar een presentatie geven gericht op metingen en communicatie van kleur. Dit doet hij namens TTMS Test & Measurement consultants.

Literatuur

• 1. H. A. Keitz, Light Calculations and Measurements, Philips Technical Library, 1968
• 2. H.J. Hentschel, Light and Lighting, Dr Alfred Huthig Verlag GmbH, Heidelberg, 1982
• 3. IES Lighting Handbook, Waverley Press Inc., Baltimore Maryland US, 1984
• 4. Wikipedia, online encyclopedia

Bron: TTMS, http://www.ttms.nl/

dr. Nebojša Fišeković, Ledivia

Dr. Nebojša Fišeković is geboren in 1969 in Belgrado, voormalig Joegoslavië. Hij heeft zijn opleiding gevolgd aan de universiteit van Belgrado, faculteit Electrical Engineering. Hij is al 15 jaar werkzaam in de lichtbranche, waarbij hij zijn ervaring hoofdzakelijk heeft opgedaan bij Philips Electronics.

Dr. Fišeković is auteur van verschillende wetenschappelijke artikelen en houder van meer dan 40 internationale patenten. Momenteel is hij werkzaam als onafhankelijk expert en consultant in de lichtbranche. In 2011 startte hij zijn bedrijf Ledivia, gericht op state-of-the-art lichtsystemen, met speciale aandacht voor lighting control systems.