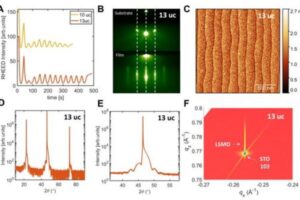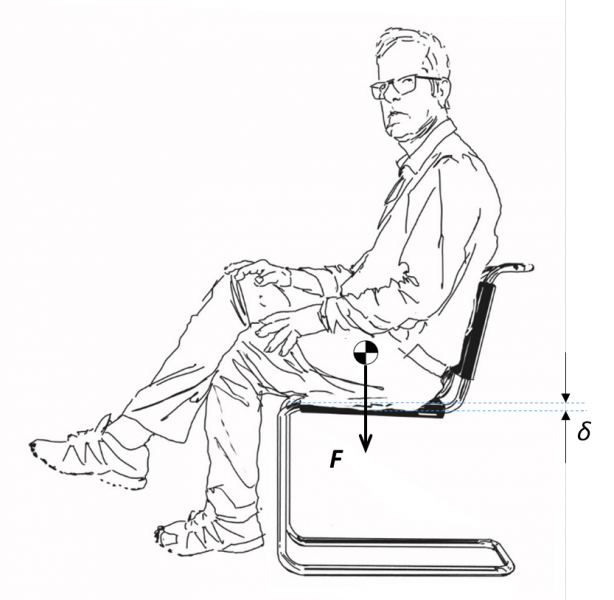
In zijn buitenaards goede essay ‘The Tyranny of the Rocket Equation’, stelt astronaut Don Petitt ons voor aan Tsiokovsky’s raketvergelijking: ΔV = Isp·g· ln(m0/mf). Deze prachtige expressie relateert de door de raket te bewerkstellingen snelheidsverandering ΔV aan de zwaartekrachtsversnelling g, de zogeheten ‘specifieke impuls’ van de gebruikte stuwstoffen Isp en de massaverhouding m0/mf. In dit laatste is m0 het startgewicht van de raket, dus inclusief stuwstoffen, en mf het eindgewicht. Die logaritme beduidt weinig goeds.
Door: Erik Tempelman, adviesbureau eriktempelman.com, universitair hoofddocent TU Delft – Industrieel Ontwerpen
Zo rekent Petitt voor dat we, om in een lage baan om de aarde te komen (ΔV = 8 km/s), liefst 83 procent van het startgewicht moeten reserveren voor stuwstoffen – en dat met de beste die er zijn: waterstof plus zuurstof. Gebruikt u de goedkopere, maar minder efficiënte combinatie van kerosine plus zuurstof, dan hebt u zelfs 94 procent nodig. De overblijvende 6 procent (of 17 procent met H2-O2) is beschikbaar voor de raket zelf – plus eventuele bemanning en andere vormen van nuttige belading, door Petitt ‘payload’ genoemd. De vergelijking houdt ons als een ware tiran gevangen op het aardoppervlak. Wie de sprong naar de ruimte wil maken heeft, zelfs bij een bescheiden payload, een reus van een raket nodig.
Ondermaanse kandidaat?
Hier op dat aardoppervlak stellen we ons nu de vraag: is er binnen de constructieleer iets vergelijkbaars te vinden voor die prachtige, maar tirannieke raketvergelijking? Een kandidaat vinden we in de ingenieurs-balkentheorie en wel d2y/dx2 = M/EI. Hieronder gaan we met deze vergelijking aan de slag. Zoals we zullen zien, wordt hiermee glashelder waarom buiging zo moeilijk te weerstaan is. En net zoals de raketvergelijking een wenselijk resultaat relateert aan de te gebruiken middelen en de bijbehorende uitdaging voor de ingenieur, zo relateert de genoemde vergelijking het wenselijke aan het mogelijke en aan de technische doelstelling.
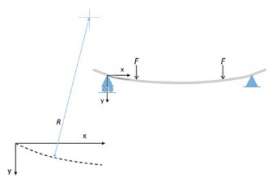 1. Kromming en kromtestraal bij een buigende balk
1. Kromming en kromtestraal bij een buigende balk
Van kromming naar vergeet-mij-nietje
In d2y/dx2 = M/EI staat de term d2y/dx2 voor de kromming van een balk als gevolg van het buigend moment M, en staan E en I respectievelijk voor de weerstand vanuit het materiaal en vanuit de vorm tegen die kromming. E is dan de materiaalstijfheid, en I is het oppervlaktetraagheidsmoment van de balkdoorsnede. Kromming mag u zien as het omgekeerde van de kromtestraal, dat wil zeggen d2y/dx2 = 1/R. U ziet een en ander terug in afbeelding 1. We hebben hier dus te maken met een differentiaalvergelijking, en wel eentje van de 2e orde.
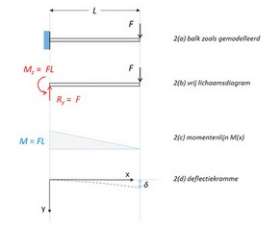 2. Nadere analyse – de eenzijdig ingeklemde balk
2. Nadere analyse – de eenzijdig ingeklemde balk
Nu is een differentiaalvergelijking een soort van ‘gezipte’ formule. Om hem te kunnen gebruiken, moeten we hem eerst ‘uitpakken’ door te integreren. Tijd voor een voorbeeld. In afbeelding 2 ziet u een éénzijdig ingeklemde balk met lengte L, belast aan het vrije einde met een kracht F. De balk heeft een constante dwarsdoorsnede en is gemaakt van één enkel materiaal: E en I zijn nu dus constant. Achtereenvolgens ziet u (a) de balk zoals gemodelleerd, (b) het vrijlichaamsdiagram, (c) de momentenlijn M(x), en (d) de vorm die de balk aanneemt, ook wel bekend als de ‘deflectiekromme’.
De momentenlijn (c) geeft op elk punt langs de balk de waarde van het buigend moment, anders gezegd, de functie M(x). Deze functie bereikt zijn maximum M = FL bij de inklemming en loopt lineair af naar nul aan het vrije einde. De bijbehorende vergelijking is M(x)=FL – Fx en we krijgen:
d2y/dx2 = (FL – Fx)/EI
Dit laat zich eenvoudig integreren, omdat zowel E als I constant zijn. We krijgen:
dy/dx = (FLx – Fx2/2 + C1 )/EI
Dit beschrijft de helling van de doorbuigende balk als functie van x, anders gezegd, de raaklijn aan elk punt van de balk. De term C1 is een integratieconstante; omdat de balk bij x=0 is ingeklemd en daar dus een helling van nul moet hebben, zien we snel dat C1=0. Nogmaals integreren levert:
y(x) = (FLx2/2 – Fx3/6 + C2 )/EI
Dit nu is de doorbuiging van de balk als functie van x, met opnieuw een integratieconstante. Ook deze is gelijk aan nul, aangezien de balk bij x = 0 nog steeds zit vastgeklemd. De doorbuiging is maximaal bij het vrije uiteinde, dus voor x = L, en als we dit invullen krijgen we tenslotte een beroemde vergelijking: het ‘vergeet-mij-nietje’:
δ = FL3/3EI
De δ staat dan voor de maximale doorbuiging. Ook handig is de maximale helling van de raaklijn:
φ = FL2/2EI.
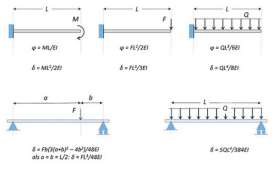 3. ‘Vergeet-mij-nietjes’ voor verschillende scenario’s
3. ‘Vergeet-mij-nietjes’ voor verschillende scenario’s
Er zijn meer vergeet-mij-nietjes. Mochten ze u even ontschoten zijn: afbeelding 3 vat de belangrijkste voor u samen. Door slim combineren kan een veelheid aan buigscenario’s worden doorgerekend. Ook het statisch onbepaald opgelegde balkje uit Not Safe For Designers – I: statica is met behulp van vergeet-mij- nietjes op te lossen.
Interpretatie: buiging versus trek
Ontwerpen op buiging is doorgaans ontwerpen op stijfheid. Het wenselijke is dan om een gegeven dwarskracht F over een lengte L door te leiden zonder dat de doorbuiging δ te groot wordt. Dit vraagt voldoende weerstand, dat wil zeggen een voldoende grote term EI.
Als we de aanvullende eis hebben dat het gewicht minimaal moet zijn, dan kunnen we afleiden dat het beste materiaal datgene zal zijn waarvoor de expressie √E/ρ maximaal is. Daarin is ρ de dichtheid van dat materiaal. Zodoende ‘wint’ aluminium het van staal: het heeft weliswaar slechts eenderde van de stijfheid van staal, maar ook eenderde van de dichtheid, en we kunnen dus bij gelijk gewicht een grotere dwarsdoorsnede maken, waardoor het oppervlaktetraagheidsmoment I zeer veel toeneemt. Die dikke buizen van uw aluminium fietsframe hebben dus hun nut. [Fietsframes worden ook op torsie belast, maar bij weerstand tegen torsie treedt hetzelfde effect op.]
Echter, dit neemt niet weg dat buiging een uiterst inefficiënte belastingsvorm is! Dit wordt duidelijk door een directe vergelijking met trek. Op trek belast zal een ‘balk’, beter gezegd: een trekstaaf, een verlenging vertonen van ΔL = FL/EA, waarin A het dwarsoppervlak is. Stel nu dat we een ronde buis nemen, met straal R = 11 mm, wanddikte t = 2 mm, en lengte L = 250 mm. Op buiging zal dit onderdeel nu ruim honderd maal meer [Om precies te zijn: 103 maal zo veel. Rekent u het gerust even na. NB: om praktisch bruikbaar te zijn, moeten framebuizen ook nog een zekere minimale wanddikte hebben, anders ‘verkreukelt’ uw frame maar al te snel als een bierblikje. Dit laatste is wat staal in vergelijking met aluminium uiteindelijk de das om doet.] vervormen dan op trek, bij dezelfde kracht F (!!). En dat terwijl een ronde buis al aardig optimaal is in het weerstaan van buiging: alleen een I-profiel doet het, per kilo gerekend, nog ietsje beter. Hebt u liever een iets kortere buis, dan wordt het verschil wat kleiner; bij langere buizen tekent het verschil tussen trek en buiging zich nog nadrukkelijker af.
Dit verbijsterende verschil is als volgt te verklaren. Een buigend moment, zo vertelt ons de oorspronkelijke differentiaalvergelijking, genereert een kromming. Zou deze kromming constant zijn, dan nog ‘plant deze zich voort’ over de gehele lengte van de balk in de vorm van een lineair toenemende helling, die op zijn beurt een kwadratisch met lengte toenemende doorbuiging δ oplevert. Neemt het moment lineair toe met L (zoals in afbeelding 2), dan zo ook de kromming, en wordt de helling een kwadratische functie… en krijgen we voor de doorbuiging te maken met een derdemacht. Het is nog net niet zo erg als die logaritme waar raketten onder lijden, maar de invloed van de balklengte L is ontegenzeggelijk groot. Bij trek zit dit anders: daar gaat vervorming lineair met L.
Liever spanningen?
Kijkt u in plaats van naar vervormingen liever naar spanningen, dan komt de inefficiëntie ook glashard aan het licht. Bij buiging ondervindt alleen het materiaal aan de boven- en onderzijde de maximale spanning, met een lineair verloop ertussen en een zogeheten ‘neutrale lijn’ ergens in het midden waar het materiaal helemaal geen spanning ervaart. En als, zoals in ons voorbeeld, het buigend moment maximaal is bij de inklemming en van daaruit lineair afloopt, dan zijn de spanningen óók alleen maximaal bij die inklemming, en aflopend naar nul bij het vrije uiteinde. Kortom: verreweg het meeste materiaal wordt amper belast. Bij een trekstaaf is dat anders – daar wordt in principe [In de praktijk is het bij een trekstaaf lastig om de kracht goed in te leiden en is efficiency niet 1-2-3 te garanderen.] alle materiaal volledig belast, en dat is veel efficiënter.
Geldigheid: aannames en randvoorwaarden
Tsiolkovsky maakte voor zijn raketvergelijking diverse aannames, zoals dat de raket slechts één trap heeft. Ervaren rakettechnici weten dat je met een meertrapsraket iets ‘verder’ komt (lees: sneller gaat), omdat je dan niet het volledige lege gewicht mee naar boven hoeft te zeulen. [Nog een voordeel: bij meerdere trappen kan de motor van elke trap geoptimaliseerd worden voor de hoogte waarop deze wordt gebruikt. En, je kunt desgewenst verschillende stuwstoffen per trap gebruiken.] En door met de aardrotatie mee te lanceren krijg je, althans op de evenaar, gratis 480 km/u cadeau: daarom zit de Nasa in Florida, en de Esa in Frans-Guyana. Geen van beide voordelen zit in de vergelijking. Maar, dat eerste stukje door de atmosfeer geeft luchtweerstand en dat zit er ook niet in, evenmin als de stuwstoffen die je, eenmaal in de gewenste baan aangekomen, voor standregeling en manoeuvres nodig hebt. In de praktijk vallen de plussen en minnen aardig tegen elkaar weg en ligt Tsiolkovsky’s benadering verrassend dicht bij de realiteit van de ruimtevaart.
Zo is het ook met de vergeet-mij-nietjes, waar weliswaar diverse versimpelingen achter zitten, maar waar toch bruikbare resultaten mee te behalen zijn. Ja, het materiaal moet zich lineair elastisch gedragen, maar dat doen technische materialen doorgaans best aardig. Ja, de lengte moet minstens het tienvoudige zijn van de hoogte van de balk, maar dat is vaak genoeg het geval. [Bij ‘korte’ balken kunnen we de effecten van afschuiving niet negeren. De Timoshenko beam theory biedt ons dan een uitweg.] Ja, diezelfde hoogte moet groter zijn dan de balkbreedte – maar opnieuw geldt dat dit meestal zo is, en anders rekent u gewoon met E(1 – ν2) in plaats van E. Prima voor boekenplanken en meer van zulk moois. En ja, de doorbuiging moet klein zijn vergeleken met de balk zelf, maar dat moet sowieso wel, omdat anders de spanningen zo groot worden dat ons materiaal gaat vloeien en dus niet meer lineair elastisch is. Nog een aanname is dat de balk bij het buigen in een (verticaal) vlak blijft liggen en dus niet ook nog tordeert – iets waar we constructietechnisch doorgaans wel voor kunnen zorgen. [Uw zoekterm: ‘dwarskrachtsmiddelpunt’. Succes.]
Alles bij elkaar genomen wordt duidelijk dat die vergeet-mij-nietjes hun plek in uw werkgeheugen dubbel en dwars verdienen. Ze vormen een stukje ingenieurswetenschap van zeldzame waarde: met een handjevol wiskunde en een paar alleszins redelijke aannames geven ze ons een prima afschatting van de te verwachten doorbuiging van constructiedelen, in allerlei vormen en onder allerlei buigbelastingen. Die schatting laat zich vaak ook prima experimenteel valideren – handig voor een college of workshop over buiging. En nu we het toch over doceren hebben: net zoals de statica een introductie biedt voor stelsels van vergelijkingen, zo biedt de ingenieursbalkentheorie een opstap naar differentiaalrekening.
Tirannie
Buiging is verder een treffend geval van ‘kleine oorzaken, grote gevolgen’. Als de Tsiolkovsky-raketvergelijking ons leert waarom raketten zo gigantisch groot moeten zijn, dan leert d2y/dx2 = M/EI ons waarom buiging zoveel harder aantikt dan trek. Het is met recht de tirannieke vergelijking in de constructieleer! Wat we daarmee aan moeten, is ons onderwerp voor de volgende keer.